続けます。
「赤い帽子の問題」(元ネタ野崎昭弘『詭弁論理学』、「その1」に旧版からの原文引用あり)は、「死刑囚のパラドックス」や「抜き打ちテストのパラドックス」とは構造を異にする問題ではなかろうか。私の結論は、構造を異にする問題だというものである。
なんとなれば、何らかの形で「死刑囚」や「抜き打ちテスト」の1日に相当するタイミングを与えれば、赤い帽子をかぶせられたプレイヤーはそれを言い当てることができるからだ。そのような行為は「死刑囚」や「抜き打ちテスト」では不可能だ。
タイミングを計る方法としては、何度か書いた「一定時間ごとにベルを鳴らし回答を促す」でもいいし、今回新たに思いついたのだが「インタビュアーが後ろから順番に帽子の色を尋ねる」というのでもいいように思う。
いちばん後ろのプレイヤーは、必ず自分の帽子の色を言い当てられる。なぜなら自分の前にいるプレイヤー全員の帽子の色が見えるから、誰かが赤い帽子をかぶっていれば白と、全員の帽子の色が白なら赤と答えればいい。
後ろから2人目のプレイヤーは、どうだろう? いちばん後ろのプレイヤーの回答を聞いた後であれば、やはり必ず自分の帽子の色を言い当てることができる。
いちばん後ろのプレイヤーの帽子の色が赤であれば、後ろから2人目のプレイヤーには順番が回ってこない。
いちばん後ろのプレイヤーが白だと答え、かつ見えている全員の帽子の色が白なら赤と答えればいい。
以下同様にn人目のプレイヤーは、もし自分に順番が回ってきて、かつ自分の目の前に赤い帽子をかぶっているプレイヤーがいなければ、自分の帽子が赤だと答えることができる。パラドックスは発生しないのだ。
後ろからインタビューしていくことは「死刑囚」や「抜き打ちテスト」ではどんな行為に相当するだろうか? タイムマシンで日にちをさかのぼれば、死刑執行日やテスト実施日を言い当てることができるかな、などと非現実的なことを少し考えたが、あまり意味がなさそうなのでやめた。
むしろ「赤い帽子」を「死刑囚」や「抜き打ちテスト」に近づけるとしたら、並んだプレイヤーの前から順番に尋ねてくことにすればいいのではないかと考えた。
ただし、いちばん後ろのプレイヤーは赤い帽子をかぶれないことにする。ルールに "誰が赤い帽子をかぶせられたかが、本人にわからないようにしなければならない" と明記されているからだ (追記:ここに自分で自分を騙す詐術が含まれていた。あとで気がついた!
「その2」の後ろの方で述べた通り、「伏せたトランプの問題」はいちばん下のカードがジョーカーでもかまわなかった。「死刑囚」や「抜き打ちテスト」の最終日は、問題文の表現によりけりだがグレー。以下、いちばん最後NG固定だとどうなるか、という考察がやりたかったのである。
もし2人しかプレイヤーがいなかったら、後ろから2人目のプレイヤーは赤の確率1(100%) だが、
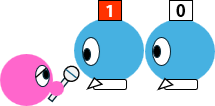
もし3人以上のプレイヤーがいた場合、後ろから3人目のプレイヤーは確率1/2(そして後ろから2人目は、1ではなく1/2!)、
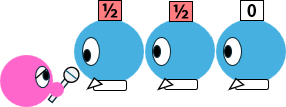
4人目のプレイヤーは1/3…
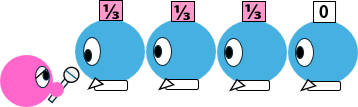
すなわちただの運ゲーになるのではないかと考えたのである。やはりパラドックスは発生しない。
なぜならプレイヤー3人以上の場合、先頭すなわち後ろから3人目以前のプレイヤーには赤い帽子をかぶっている可能性が自分自身と後ろのプレイヤーにあり、判断できないからだ。
これってば、プレイヤー2人の場合とプレイヤー3人以上の場合はそれぞれ異なる状況であって、プレイヤー2人の場合で考察した結果をプレイヤー3人以上の場合に適用できないことの具体例にならないだろうか。
こんなふうにシチュエーションをいろいろ変えることにより考察を深めることは、なにがしかのご利益があるように思われる。
ただし、あれこれ考えているうち「そもそもパラドックスって何だったっけ?」という疑問が色濃くなってきた。
「赤い帽子の問題(前から訪ねていく)」も「伏せたトランプの問題」も、運ゲーではあってもパラドックスではない。「赤い帽子の問題(後ろから訪ねていく)」は、正解があるパズルである。
ではなぜ「死刑囚のパラドックス」や「抜き打ちテストのパラドックス」はパラドックスなのだろうか? 少なくともパラドックスと感じられるのだろうか?
別人がやると別物になる法則。ネギ(id:ad2217)さんが提唱された「おもちゃの機関車が爆弾のスイッチを押していく問題」、読ませていただきました。通知お騒がせします。
私の分類だと「おもちゃの機関車問題」は「伏せたトランプ問題」と同じ「最後の箱が爆弾でもOK」の運ゲーになります。論点の設定が、ネギさんと私では違っているようです。
だんだん問題のありかが絞り込まれてきたような気がした。もう一考えしなければならなそうだ。だけどまだ結論には至っていない。連続投稿はできないけど、この項まだ続けるかも知れません。
追記:
もう一言。今回の考察で、重要なヒントが得られたように思われた。
結論を先に書けば、例外的なプレイヤーには「自分の帽子の色が赤だとわかる」と「赤い帽子をかぶせられない」が両立しない場合があるということだ。それを認めなければ、ゲームが成立しない。
プレイヤーが3人以上の場合、後ろから2番目のプレイヤーは、いちばん後ろのプレイヤー同様、必ず自分の帽子の色がわかってしまう。
だが後ろから2番目のプレイヤーに赤い帽子をかぶせられる可能性を残すことによって、運ゲーとしてのゲームが成立するのである。
もし、いちばん後ろのプレイヤーに赤い帽子をかぶせることを禁じたのと同じ理由で後ろから2番目のプレイヤーにも赤い帽子をかぶせることも禁じたら、同様の理屈で3番目のプレイヤーにも赤い帽子がかぶせられなくなる。無限ループが生じて、どのプレイヤーにも赤い帽子をかぶせられなくなる。これが「パラドックス」の状態ではなかったか。
例外的なプレイヤーは、もともと存在する。このゲームでは、いちばん後ろのプレイヤーがそれだ。もしプレイヤーがいちばん後ろの1人だけだったら、「自分の帽子の色が赤だとわからない」というルールは成立しない。だが「もしプレイヤーが1人だったら」という考察抜きには、推論は始まらない。
後ろから2番目のプレイヤーに対しても、その例外性を認めることによりゲームが成立するのではないか。
そうすると、いちばん後ろのプレイヤーから今回付与した「赤い帽子をかぶせられない」という例外性を取り除き、代わりに後ろから2番目のプレイヤーに与えた「『自分の帽子の色が赤だとわかる』からといって『赤い帽子をかぶせられない』ことはない」という例外性を与えると、どうなるだろう? それがまさしく「死刑囚のパラドックス」や「抜き打ちテストのパラドックス」と等価のパズルになるのではなかろうか。
「伏せたトランプ」の問題とも、等価なのではなかろうか? カードが1枚だけだったら「それがジョーカーだとわかる」。だが「それがジョーカーであってはならない」ということには、ならない。
つかもともとこの例外性は、いちばん後ろのプレイヤー特有のものだったようだ。それが「いちばん後ろのプレイヤーには赤い帽子がかぶせられない」というルールを追加することで、後ろから2番目のプレイヤーに移動しそれによって可視化された(目立つようになった)とは言えまいか。
追記の追記:
いちばん後ろのプレイヤーの例外性は「自分の帽子の色がわかる」ないし「自分の帽子の色がわからないようにかぶせることはできない」であって、「赤い帽子をかぶせることはできない」ではないのだ。「赤い帽子をかぶせることはできない」のと同様、「白い帽子をかぶせることもできない」のだ!
この誤解ないし混乱が、パラドックスの根源だったのかも知れない。
追記の追記の追記:
追記まとめました。
弊ブログはアフィリエイト広告を利用しています
