少し間が空いてしまったが、1月28日付のこの拙記事にタラタラと追記した内容をまとめる。
まずは「死刑囚のパラドックス」ないし「抜き打ちテストのパラドックス」の等価と思われる「赤い帽子の問題」を、もう一度手短かに説明する。
一人の被せ手と、複数のプレイヤーがいる。
被せ手は、プレイヤーの人数分の帽子を持っている。1つだけが赤で、残りはぜんぶ白である。
被せ手は一列に並んだプレイヤーに、帽子を被せていく。プレイヤーは自分の前に並んだプレイヤーの帽子の色は見えるが、自分の帽子と自分の後ろに並んだプレイヤーの帽子は見えない。
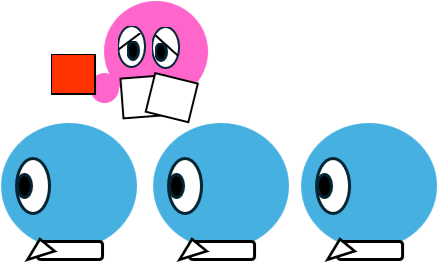
被せ終ったら、被せ手はプレイヤーの先頭からから順番に、自分の帽子の色が赤白どちらか質問していく。
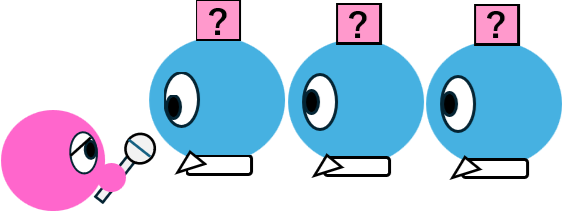
このゲームのキモは、
「被せ手は、プレイヤーに自分の帽子の色がわからないように被せなければならない」
ということである。
もしプレイヤーが自分の帽子の色を言い当てることができたらプレイヤーの勝ち、できなかったら被せ手の勝ちということにする。
次のように考えると、このゲームはプレイヤー必勝、被せ手必敗のように思える。
列の一番後ろに並んだプレイヤーは、必ず自分の帽子の色を言い当てることができる。
なんとなれば、もし自分の前のプレイヤーの誰かが赤い帽子を被っていたら、自分の帽子は白だとわかる。
もし自分の前のプレイヤー全員が白い帽子を被っていたら、自分の帽子は赤だとわかる。
拙過去記事においては、以上の推論によって
「一番後ろのプレイヤーに赤い帽子を被せることはできない」
と結論し、次の推論に移行したが…
この結論は、間違っていたのではないか?
この推論によって導かれる結論は
「一番後ろのプレイヤーには、赤い帽子も白い帽子も被せることはできない」
というのが正しいのではないか?

弊ブログはアフィリエイト広告を利用しています
いちばん後ろ以外のプレイヤーのことを一旦失念すると、これは古典的なパラドックスである「嘘つきのクレタ人のパラドックス」あるいは「村に一人しかいない床屋のパラドックス」と相似形になるのではなかろうか? すなわち、2択のどちらを仮定してもルール違反になるという形式である。
あるパラドックスを論じるのに次々と別のパラドックスを持ち出すのは、永久ループつか無限後退のようで、若干気が引けるけど。
村に一人の床屋のパラドックスというのは、次のようなものだった。
ある村には、床屋が一人だけいる。
1. この村では、自分のヒゲを剃らない村民のヒゲは、床屋が剃る
2. 自分のヒゲを自分で剃る村民のヒゲは、床屋は剃らない
この床屋は、自分のヒゲを誰が剃るのか?
もし自分で剃るとしたら、2.に違反する。よって自分で剃ることはできない。
もし自分で剃らないとしたら、村には床屋は自分一人しかいない。よって1.によって自分で剃らなければならない。
村に一人の床屋のパラドックスに関しては、どの本だったか忘れたがヒゲを伸ばし放題にした床屋のイラストを載せていた本があったが、それも間違いで「床屋は『自分の髭を剃らない』こともできない」のだから、そのイラストは誤りではないかということを2023年10月22日付拙記事に書いたことがあった。ええっ、足掛けもう2年前??
しかし人間の思考にはクセのようなものがあって、村に一人の床屋のパラドックスに関しては「自分のヒゲを剃らない床屋」をイメージしがちである。
「赤い帽子の問題」に関しては、ごく自然に「いちばん後ろのプレイヤーには赤い帽子を被せられない」ことをイメージしてしまった。
だが「赤い帽子を被せない」ことは「白い帽子を被せる」という具体的な行動と対等である。これにより、パラドックスの本質あるいはツボがこのあたりにあるのではないかと気づくことができた。
ここまで考えなければわからなかったのって、私だけ?
後ろから2番め以前のプレイヤーについても、考察しておかなければならない。
一番後ろのプレイヤーには、とにもかくにも帽子を被せてしまうことにする。ただし一番後ろのプレイヤーに被せた帽子の色は、赤白どちらかわからない。
なぜなら、一番後ろのプレイヤーに赤い帽子を被せても、白い帽子を被せても、全員に帽子を被せ終わった時点で一番後ろのプレイヤーには自分の帽子の色がわかってしまうのだが、これは「どちらの帽子を被せても『自分の帽子の色がわからない』というルールに反する」という意味であって、赤白どちらかの特定の色の帽子を被せてはならないという理由にはならないからだ。
ゲームを進めるためには、被せ手は赤か白かどちらかの帽子を被せるしかない。

以前のエントリーでは、一番後ろのプレイヤーの帽子の色を白(赤であってはならない)と仮定すると、2番目のプレイヤーにも自分の帽子の色がわかってしまうと結論した。
すなわち自分の前のプレイヤーの誰かが赤い帽子を被っていたら、自分の帽子は白。もし全員が白い帽子を被っていたら、自分の帽子は赤。
ところが一番後ろのプレイヤーの帽子の色が白という仮定が崩れたのだから、自分の帽子の色は確率的にしかわからないことになる。
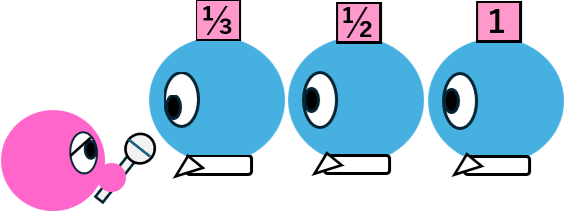
そうすると、後ろから2番目のプレイヤーに質問の順番が回ってきたとき、プレイヤーが赤い帽子を被っている確率は1/2、
後ろから3番目のプレイヤーに質問の順番が回ってきたとき、そのプレイヤーが赤い帽子を被っている確率は1/3、
後ろからN番目のプレイヤーに質問の順番が回ってきたとき、そのプレイヤーが赤い帽子を被っている確率は1/N、
一番後ろのプレイヤーに質問の順番が回ってきたときに、一番後ろのプレイヤーが赤い帽子を被っている確率は1/1=1。
すなわちこのゲームは、ただの運ゲーということになる。パラドックスは発生しないのだ。
ただしこれらの数字は、ベイズ理論でいう事後確率であることに注意。事前確率を言えば、すなわち被せ手が先頭から順に質問を始める前に、N人のプレイヤーがいれば各プレイヤーの帽子の色が赤である確率は、全員が等しく1/Nである。ベイズ理論言いたかっただけですすみません。
…と言いつつ、ベイズ理論でこのパラドックスの解釈を試みるという手もあるのか。一番後ろのプレイヤーに帽子の色がわかってしまうといういことは、一番後ろのプレイヤーの事後確率が1になると言い換えることもできる、とか何とか。
弊ブログはアフィリエイト広告を利用しています
以上の反省を、死刑囚のパラドックスや抜き打ちテストのパラドックスに対しても、適用してみよう。
抜き打ちテストのパラドックスについて考えてみる。
教官が生徒に告げた。
i. 今週金曜日までに抜き打ちテストを実施する
ii. いつ抜き打ちテストを実施するかは、生徒にはわからない
前半の「赤い帽子の問題」への考察を、この問題に翻案するとしたら、次のようになる。
「プレイヤーは『赤い帽子を被せられる』か『白い帽子を被せられる』かの2択である」ということとと、「週内のある日に『抜き打ちテストが実施される』か『抜き打ちテストが実施されない』かの2択である」ということは等価である。
「一番後ろのプレイヤーには、前のプレイヤーの帽子が見える」ということと、「最終日には、それ以前に抜き打ちテストが実施されたかされなかったかわかる」ということは等価である。
そうすると、「最終日には抜き打ちテストが実施できない」とだけ予想することは誤りになるのではないか? 正しい推論は「最終日には『抜き打ちテストが実施される』と予想するのも誤り、『抜き打ちテストが実施されない』と予想するのも誤り」ではないのか?
もし木曜日まで抜き打ちテストが実施されなかったら(目の前の帽子がぜんぶ白)、金曜日に抜き打ちテストが実施される事後確率は1すなわち100%だとわかる(一番後ろの帽子が赤
だが、このことをもって「最終日の金曜日には抜き打ちテストが実施できない(一番後ろの帽子が赤であってなはらない)」と結論することは、誤りである。
なぜなら、もし木曜日までに抜き打ちテストが実施されたら(目の前の帽子のうち一つが赤)、金曜日に抜き打ちテストが実施される事後確率は0すなわち0%なのだから「抜き打ちテストを実施しない」ことが、わかってしまう(一番後ろの帽子が白
よって「最終日の金曜日には『抜き打ちテストを実施しない』こともできない(一番後ろの帽子が白であってなはらない)」と結論することも、できてしまう。
あえて結論づけるとしたら、ii.に矛盾しないためには「最終日には『抜き打ちテストを実施する』ことも『抜き打ちテストを実施しない』こともできない」とするしかないのではなかろうか?
この結論を、より自然な言い回しに言い換えると「最終日には『抜き打ちテストが実施される』か『抜き打ちテストが実施されない』かが、必ずわかる(のでii.は成立しない)」という、ごくごく平凡なことを言っているにすぎなくなる。
ありゃりゃ、なんでこんなに、わかりにくくなってしまうの??
うーん、「抜き打ちテストを実施する」という「具体的な行動の肯定」と「抜き打ちテストを実施しない」という「具体的な行動の否定」を並べて、これらが対等だと述べることは、
さきの「赤い帽子を被せる」と「白い帽子を被せる」(どちらも具体的な行動)を並べて、これらが対等だと述べることに比べると、わかりにくいのかな?
ひょっとしたら、ベイズ理論に基づく説明の方が、わかりやすいかも知れない。「ベイズ理論」というものものしい言葉が、読者の「この説明を読んで理解しよう」という意思をくじく側面なきにしもあらずかも知れないが。
もし金曜日以前に抜き打ちテストが実施されていれば、金曜日に抜き打ちテストが実施される事後確率は0である。
だが、抜き打ちテストが実施された後のことは、最終日に限らず意識に上りにくい。
週末までの日数がN日であれば、最終日を含めた各日に抜き打ちテストが実施される事前確率は1/N、1日が経過するたびにNが1ずつ減ってゆき、最終日まで抜き打ちテストが実施されなかったケースすなわちN=1の場合の事後確率が1/1=1=100%になるというだけで、パラドックスは発生しないのだ。
事前確率と事後確率の混同が、パラドックス発生の原因なのかも知れない。
ベイズ理論云々については、例によってこの文章を書いているうちに思いついた。そういうことが、本当によくある。
