自己満足的数独(ナンプレ)のプレイ記録である。前回はこちら。
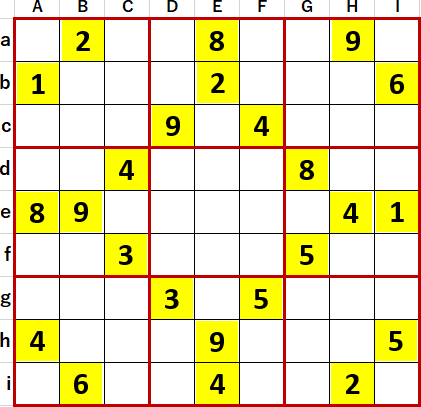
特徴的な問題に遭遇したので、自分用に記録する。ニコリ『超激辛数独4』P87 80。作者 我ヒトにあらず さん。難易度Level10+。初期値を背景色黄色で示す。
弊ブログはアフィリエイト広告を利用しています
初等解法で埋められるマスを埋め、埋められないマスには候補として入りうる数字のメモを書き尽くしたのが次図。この状態を導くにあたって5の井桁を使ったが、説明は省略する (Aa・Ca・Ai・Ci 列方向単純井桁
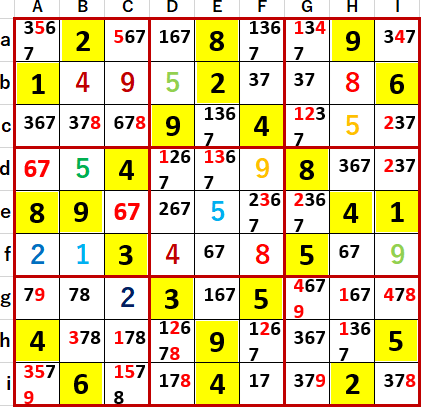
この状態から井桁チェックを行ったところ、Fb・Gb・Fe・Geに3の行方向単純井桁を見つけた。併存する列方向井桁は(BEH・cdh)の3連井桁である。
これらの井桁により空白マスに入りうる候補の数字から3を除外すると、Aa・Ia・Ai・Iiに3の単純井桁が残存した! すなわち1局面で3つの井桁が併存していたことになる。レアケースだが、こうした事例は過去にもなくはなかった。
状況を進行させよう。この結果を受けてAc・Adに6・7 2国同盟、Ic・Idに 2・7 2国同盟が発覚した。これらによりA列とI列からいくつかの候補の数字、とりわけ初期値に現れなかった7をいくつか除くことができた。

その結果Agに9が確定し、その影響でGiにも9が確定した。
さらにAc・Ad・Ic・Idに7の行方向単純井桁が見つかった。これによりc行とd行の候補から多数の7を除外することができた。
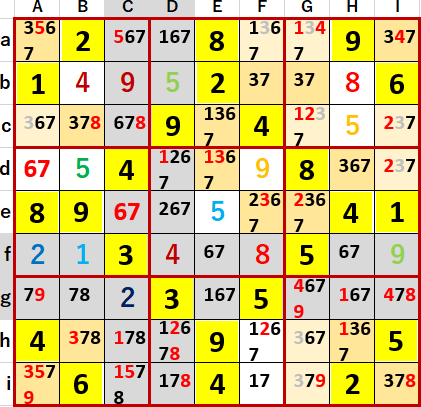
これで多重選択の連鎖的解消が始まるんじゃないかと思った。
ところが始まらなかった。さすが91問中80問目の終盤戦、手ごわい。
ここで長考に入った。1~9の井桁を再チェックしたり、N国同盟(予約)を洗い出そうとしたり。
結論を述べる。前掲スクリーンショットの7の併存井桁を確認したところ、それがさらに2つの井桁に分解できることがわかった!

すなわち併存するのは(BCDEFGH・abefghi)の列方向7連井桁(!)だったのだが、それがさらに(BEH・fgh)列方向3連井桁と(CDFG・abei)行方向4連井桁に2分できることに気づいた!
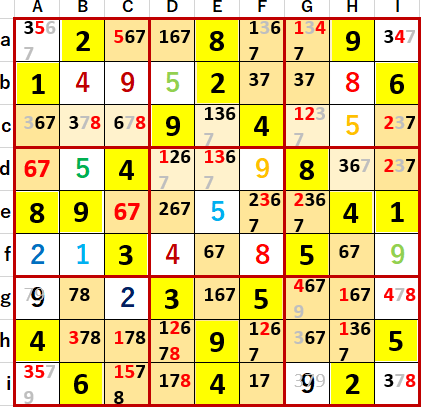
この結果Ghに6が確定したことをきっかけに、ようやく多重選択の連鎖的解消が始まってくれた。
得られた最終形のスクショを示す。Solutions P121と一致している。
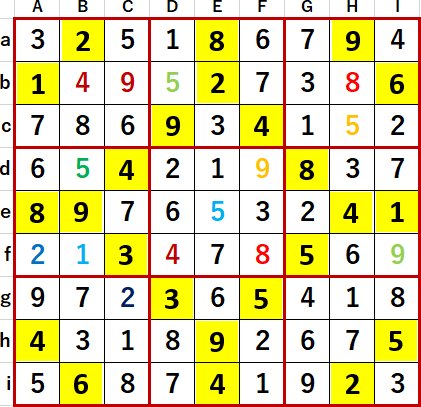
この問題の特徴は、サブタイトルに掲げた通り、1シーンで3つの井桁が同時に出現するというレアケースが2度も発生したことだった。
つか分割した井桁が、さらに分割できたことを面白がるべきか。そんなこと、これまであったっけ? たぶん初出のはず。
ただしP121のヒントには…
Fb・Gb・Fe・Ge…3井桁
Aa・Ia・Ai・Ii…3井桁
Ac・Ad…6・7予約
Ic・Id…2・7予約
Ac・Ad・Ic・Id…7井桁
7→Bg・Bh、Di・Fi→Ef…7
と書いてあった。
1行目と2行目は3枚目(5枚上)、3行目と4行目は4枚目(4枚上)、5行目は5枚目(3枚上)のスクショに、ぞれぞれ対応している。
6行目すなわち最終行は、どう解釈したらいいのだろう?
6枚目(2枚上)のスクショにおいて、B列で7の候補はBgとBhにしか残っていないから、Ciには7は入らない (もし入れたらB列で7が不足する
するとi行で7の候補はDiとFiにしか残らなくなるから、Egに7を入れることができず、E列でEfに7が確定するという意味だと理解した。すなわちニコリさん呼称「どっちにしても理論」を駆使することにより、最終形を導いているようだ。
