数独(ナンプレ)の自己満足的プレイ記録である。前回はこちら。
今回はニコリ編著『ポケット数独 上級篇』(ソフトバンク クリエイティブ) P18の問11を解いてみた。難易度は難しい方から3番目のLevel7にもかかわらず、これまで何回か常用してきた解法の範囲では解けなかった。今回はgifアニメを3枚作った。
目次
- 一択による空白マスつぶし。とりわけ「どっちに入ってもこっちしか残ってないだろう」連続使用(gifアニメ2枚)
- 新しい1択解法名付けて「総消去法」(gifアニメなし)
- 決定打は2択からの矛盾導出しか見つけられなかった(gifアニメ1枚)
一択による空白マスつぶし。とりわけ「どっちに入ってもこっちしか残ってないだろう」連続使用(gifアニメ2枚)
まずは弊ブログローカル呼称「飛車にらみ」で埋められる空白マスを埋めるところを。飛車にらみとは、特定の数字の入ったマスの上下左右をサーチし、その数字のない3×3ブロックにその数字を入れられるマスが1つしかないところを探すことである。飛車にらみで埋められるだけ埋めたところが、実質スタートのようなものである。
この問題を解いてみて最初の特徴と思ったのは、ローカル呼称「どっちに入ってもこっちしか残ってないだろう」を連続使用したことだ。
その様子を2枚目のgifアニメにまとめた。
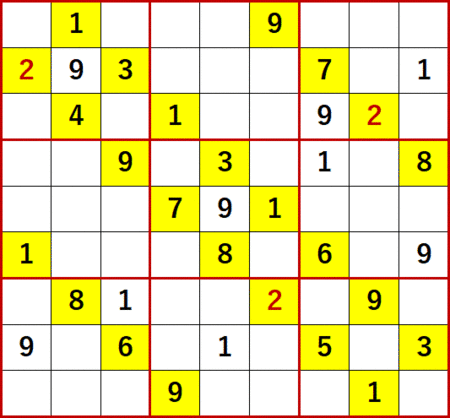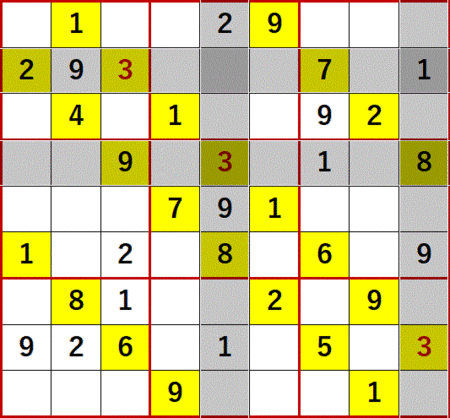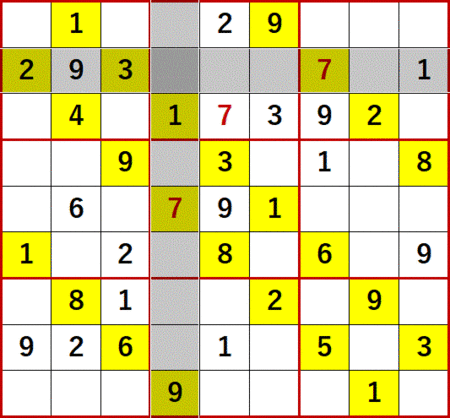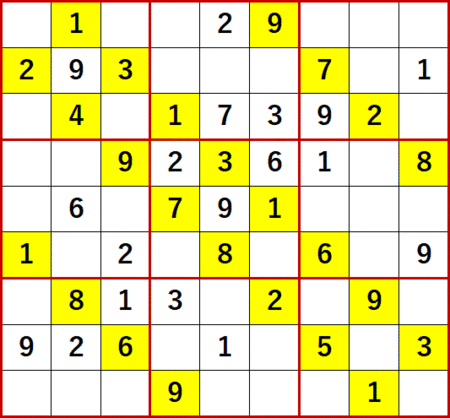
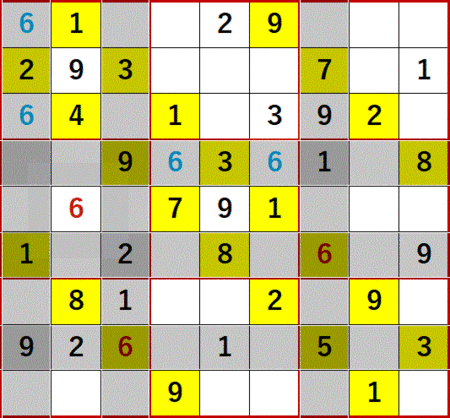
どっちに入ってもこっちしか残ってないだろうと呼んでいる解法の復習つか確認のため、静止画をいくつか貼る。
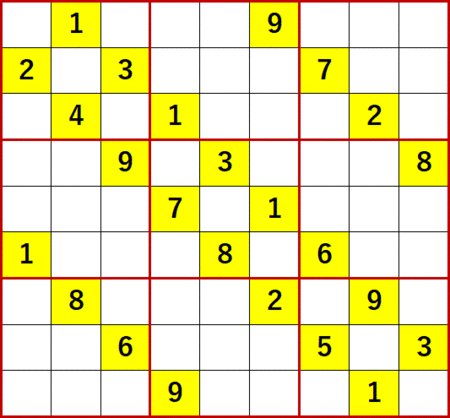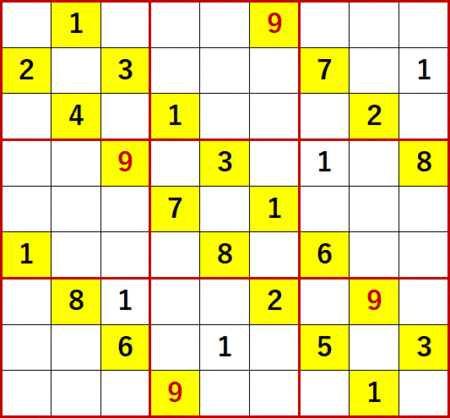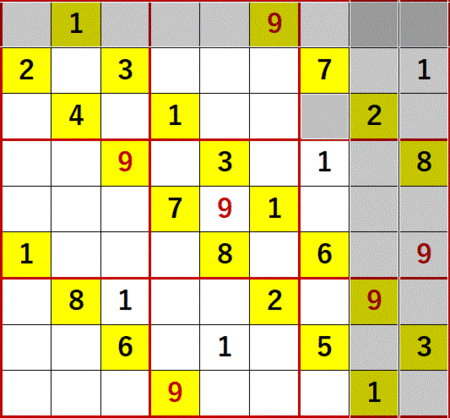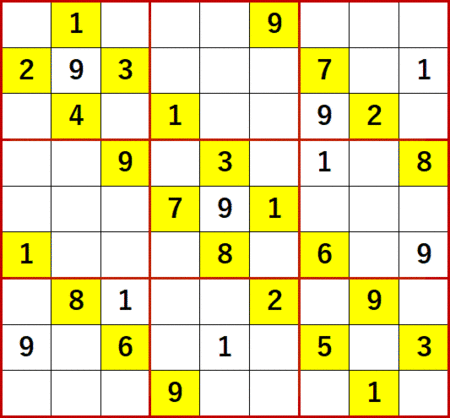
2の飛車にらみを調べると、3×3ブロック中で一つの空白マスを特定することはできないが、同一の3×3ブロック中縦に2つまたは横に2つのどちらかにしか入らないケースが発生することがある。
下図において、中央下段の3×3ブロック中に青文字で示した縦2つの2、左側下段の3×3ブロック中にやはり青文字で示した横2つの2が、それである。
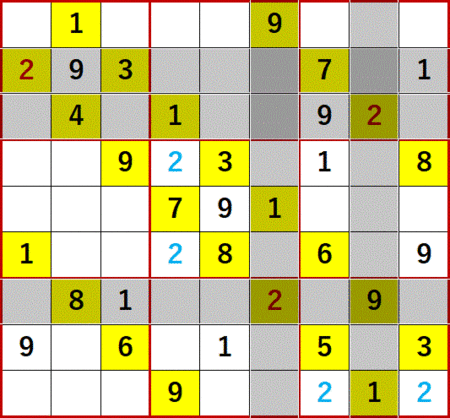
同一3×3ブロック中に縦2つ並んでいる場合は縦方向に、横2つ並んでいる場合は横方向に飛車にらみを利かせることができる。
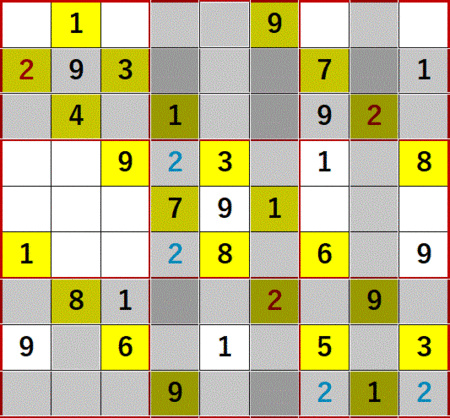
他のすでに決定している2も利用して、中央中段3×3ブロックの縦2つの2により中央上段3×3ブロックの2が、右側下段3×3ブロックの横2つの2により左側下段3×3ブロックの2が決定するのである。
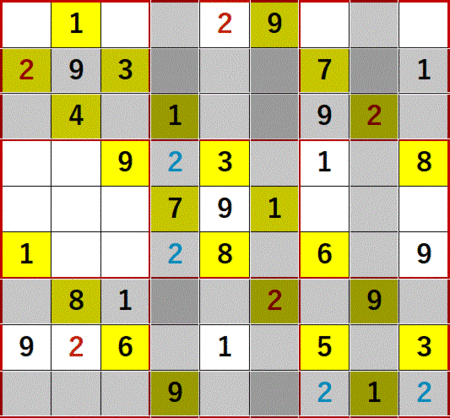
一度に2ケースを示すのは、わかりにくかったかも知れない。ふつうは一度に1ケースの「どっちに入ってもこっちしか残ってないだろう」が発生するものであり、そういう例は過去記事に何度か示しているのでそちらを参照していただければ。
次に示すのは、縦横2ケースに同時に発生した6を縦横で利用して、右側中段の6を特定しているところである。
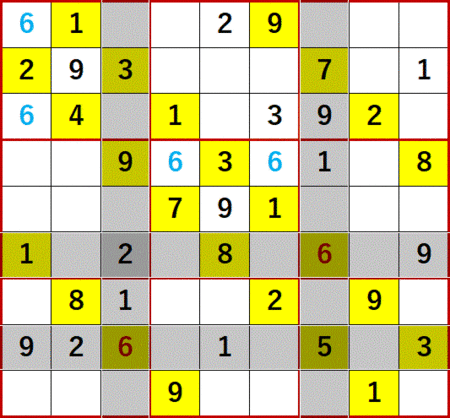
新しい1択解法名付けて「総消去法」(gifアニメなし)
飛車にらみと「どっちに入ってもこっちしか残ってないだろう」、それから今回は例を示していないがローカル呼称「一気通貫」は、どれも空白セルに入る候補として1種類の数字のみを検討する解法である。これらをまとめてやはりローカル呼称で「1択」と呼んでいる。2枚目のgifアニメは「どっちに入れてもこっちしか残ってないだろう」使用後、1択で埋められるところまで埋めている。
1択の解法はこの3つくらいかなと思っていたら、これまで使ったことのない方法で数字が特定できるケースに出くわした。
右から3列目と下から3行目の交差する空白セルに着目する。
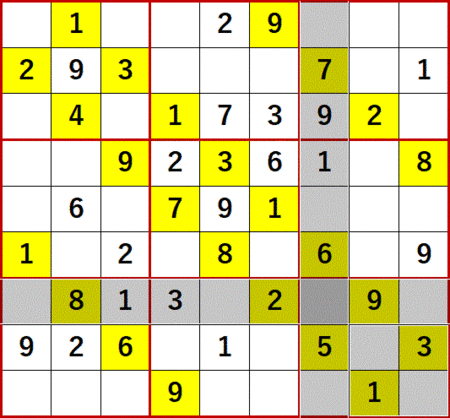
1は右から3列目、下から3行目、左側下段3×3ブロック中のいずれにもある。
2は下から3行目にある。
3は下から3行目と左側下段3×3ブロック中にある。
5は右から3列目=左側下段3×3ブロック中にある。
6は右から3列目にある。
7は右から3列目にある。
8は下から3行目にある。
9は下から3行目=左側下段3×3ブロック中にある。
よって右から3列目と下から3行目の交差する空白セルには、4しか入れられない!
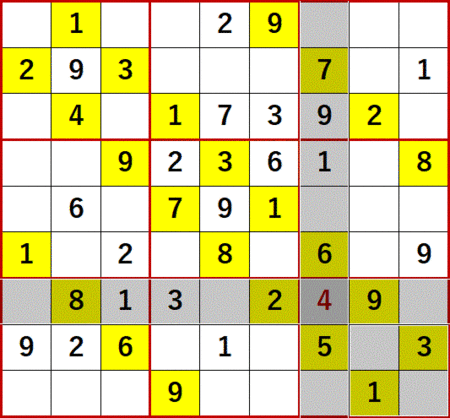
これは1択解法の一つに違いないが、飛車にらみ、一気通貫、「どっちに入ってもこっちしか残ってないだろう」いずれにも分類できない。
明らかにレアケースだと思われるが、こんなことがまた出てくることあるだろうか?
名づけるとしたらなんと名前をつけよう?
「総消去法」?
そうしょうきょほう、そうしょうきょほう、そうしょうきょほう…言えない(汗)。
早口言葉みたい。気に入った! ローカル呼称これで行こう。
でもまた出てくるかな? そうしょうきょほうと言いたいからまた出てきてほしい。
だが残念ながら、この総消去法によって新たに埋められるようになる空白マスは発生しなかった。なんとなくそんなものだろうという気がした。総消去法の適用が可能ということは、そのマスが孤立しているということだ。だから他のマスへも影響を与えられないのだろう。断言するためには証明が必要だが。
決定打は2択からの矛盾導出しか見つけられなかった(gifアニメ1枚)
これまでの問題であれば、一択により埋められる空白マスを埋めた状態から、入れられる数字の候補が2つである空白マスを特定できるだけ特定することにより、正解を導くことができた。
弊ブログでは空白マスに入る候補の数字が2つである場合を、短く「2択」と呼称している。同様に候補の数字が3つである場合を「3択」、4つの場合を「4択」と呼ぶことにする。
ところが今回の問11では、2択マスをぜんぶ数え上げ、3択マスをだいたい数え上げても、手がかりらしきものが見つけられなかった。だいたいと書いたのは、たぶん全部ではないから。
1択の場合は1~9の9種類の数字を検討すればいいが、2択では9C2=36種類、3択では9C3=81種類の組み合わせを検討しなければならなくなるから、難易度が格段に高くなると感じる。ミスも多くなる。
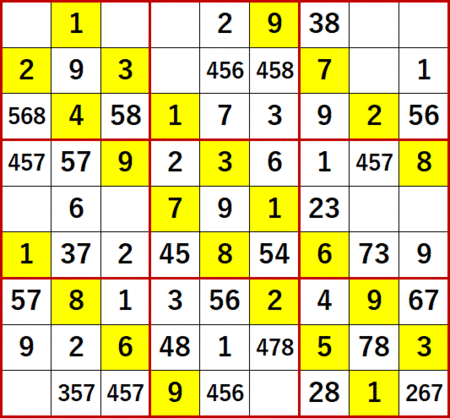
だがこの問題では、ここまでやっても手がかりが見えてこなかった。
結論を書くと、2択で矛盾が発生したら引き返すという、今年の夏に数独エントリーを再開したときの最初の拙記事の手段を用いるしかなかった。もしもっとスマートな方法がおわかりの方いらっしゃいましたら、ぜひご教示ください。
右側下段3×3ブロック中どの2択マスを選んでも同じ現象が発生するが、右から3列目いちばん下の行の2または8で、8を選んでみると…
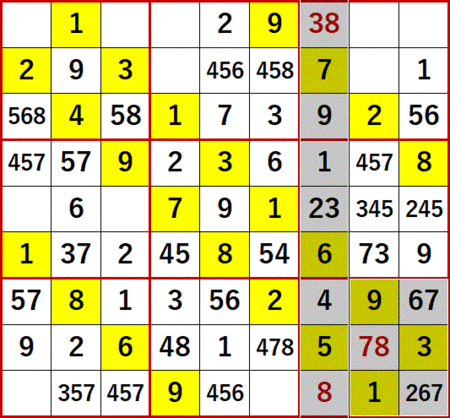
右から3列目いちばん上の行の3が決定し…
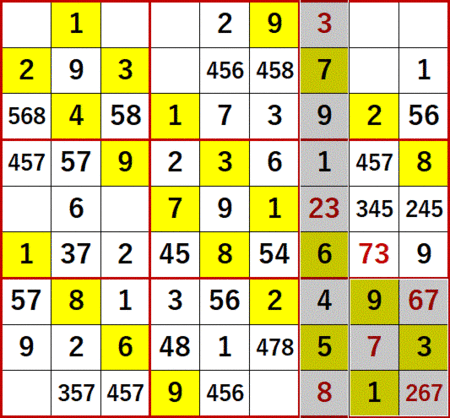
右側中段3×3ブロック中の2が決定することにより…
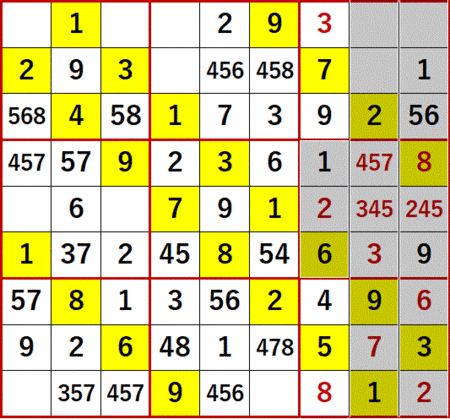
同3×3ブロック中で4か5しか入らない空白マスが3つ発生する。あるいは7がどのマスにも入れられない。
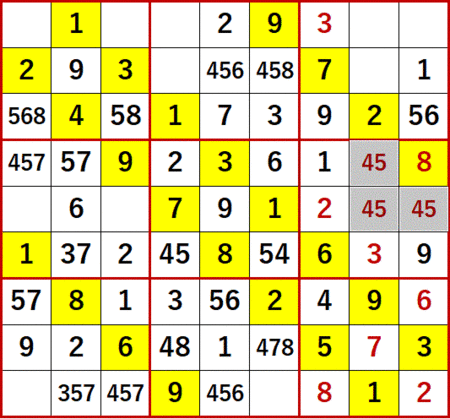
よって消去法により2を入れると…
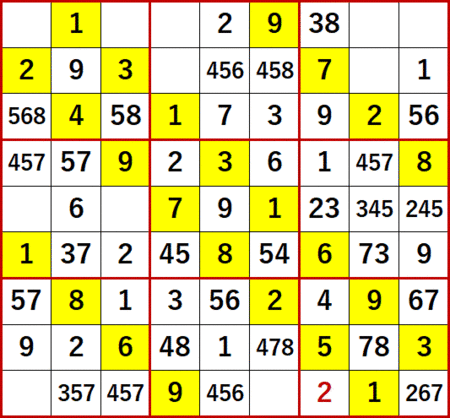
以降は3枚目のgifアニメで示す。
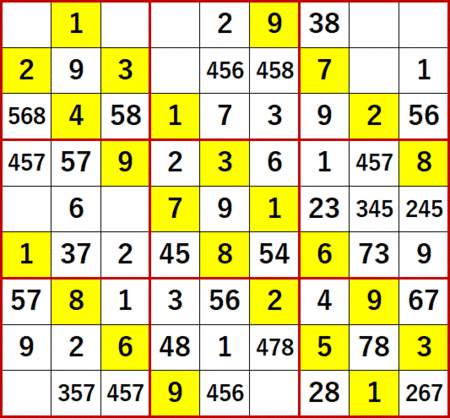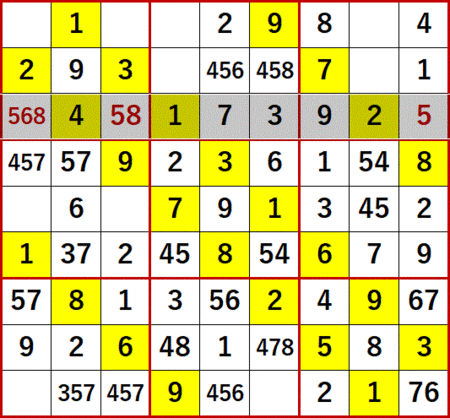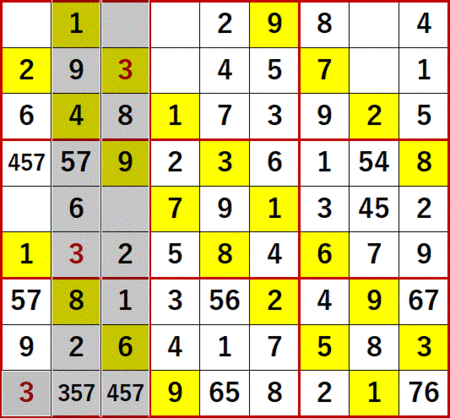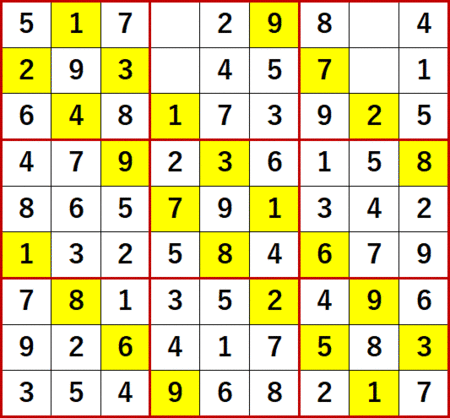
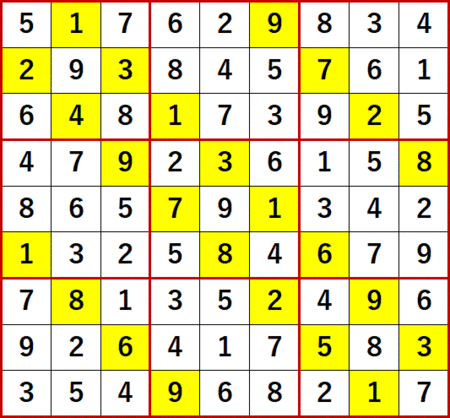
これまで同様、gifアニメは最後まで行っていない。これまで同様、得られた解答編P115と一致するスクショを最後に貼る。
追記:
連携機能で流したツイートに、ライナス @Linus_MK さんからリプでご教示いただきました。ありがとうございました。リンク失礼します。
ほぼ「2択の1つを進んでみて背理法」と同値だと思いますけど……
— ライナス (@Linus_MK) 2022年8月29日
右の中央の3×3に注目すると、7の入るのは2箇所しかありません。どちらにせよ、右から2列目なので、右から2列目に他に7は入れられません。ということは右下3×3の真ん中「78」のマスに7は入れられないので8確定です。
あわわ、弊ブログのローカル呼称で言う「どっちに入ってもこっちしか残ってないだろう」による「2択」つぶしです。今回エントリー前半であれだけ「どっちに入ってもこっちしか残ってないだろう」を連呼しておきながら、なんで気づかなかったのだろう…??
スポンサーリンク
