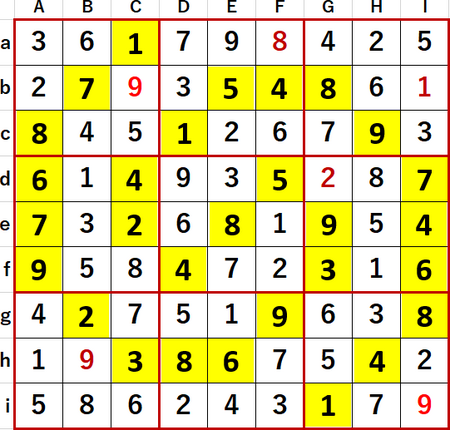
昨日付拙エントリーで「1つの問題中に同時に2つの井桁が成立するとき、どちらの井桁に着目しても除外できる数字の候補は同じ」という経験則(?)を述べ、証明できるかも知れないと書いた。
だがもう少し考えてみたら、証明は難しく、一般的には成り立たないと考えた方がよさそうだと思えてきた。
以下の図中に登場する〇✖●は、すべて同じ数字を表す。
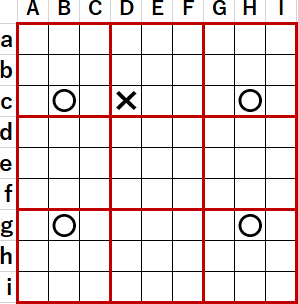
まず仮にBc・Bg・Hc・Hgに単純井桁(X-Wing)が成立していたとする。
空白セルDc(図中✖)の候補に、単純井桁を構成する数字と同じ数字が含まれていたら、単純井桁はこの候補を消す。これだけであれば、何の不思議もない。
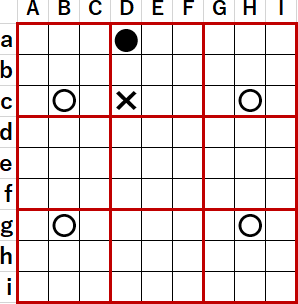
では井桁によって消えない候補が残るのはどんな場合か? 例えば次図中Daの●のように、井桁の外部に単独の候補が残ることはない。✖が消えたことにより●の表す数字が確定するからだ。それはそれでありうることであり、解決に向かうのだからめでたいことである。
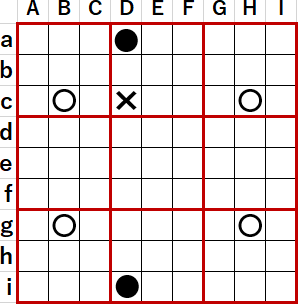
それなら次図の例ように、井桁の外部の同じ列に2つ(以上)の候補が残るケースがありうるかというと、これもありえない。この例ではa行i行それぞれ候補が1つのマスにしかないので、それぞれのマスで候補の数字が確定することになるからだ
井桁の外部で候補の数字が残る1つのパターンとして、井桁の外部の同じ行同じ列にそれぞれ2つ(以上)の候補があるケースが考えられる(Da、Di、Fa、Fi)。これがまさしく2つの井桁が同時に成立するケースであり、二つの井桁の交点の候補が消えると考えれば「どちらの井桁に着目しても消せる候補は同じ」という命題は自明のようにも思える。
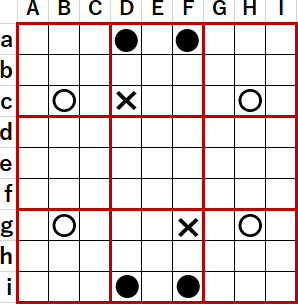
なお以上の議論は井桁の行方向に存在する候補について考察したが、盤面(って言うのか?)を左でも右でも90°回転させれば、同じ議論が列方向でも成立することは容易にわかる。
ところがこれで全てのケースを網羅しているかというと、そうではない。井桁を構成している候補以外の候補がデタラメに、すなわち井桁を構成しないような配置に分布しているケースだって、ありそうに思われる。
次図は私が今適当に思いついたものなので、現実にこのようなことがあるかはわからない。言いたかったことは、次図では●は3行4列にわたって分布しているので井桁を構成しない、ということである。
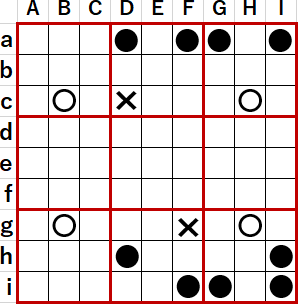
そのようなケースは十分ありそうに思われるのだが、単に検証した事例の件数が少ないので出くわしていないだけだろうか?
なんとなくそんな気がする。出くわしたら出くわしたでネタになるから、ま、いいか。私以外にそんなことを面白がる奴がいるかどうかは、さて措く。
発端となったニコリ『超激辛数独1』P78の71を再検討してもよかったが(4月29日付拙記事。4連井桁で解いたと思ったら3連井桁と解釈することもできたという問題である。その後井桁をもう1組見つけた)、どうせなので別の問題を解いてみた。
P79の72、難易度はLevel10+、作者は G さん。初期値を背景色黄色で示す。
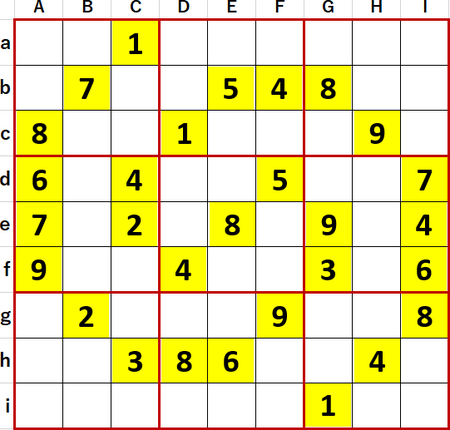
「2択先書き法」とローカル呼称している解法で確定できる数字は確定し、確定できないマスには候補の数字のメモを書き尽した状態を、次図に示す。
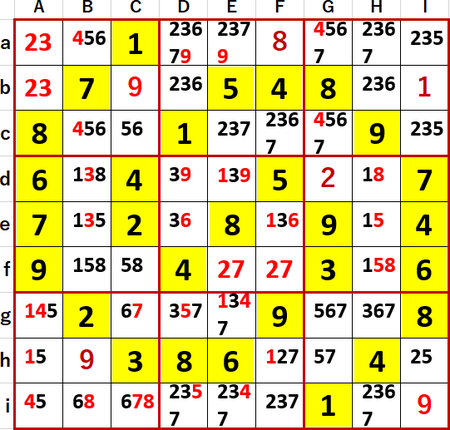
Solutions P119のヒントには…
Bi・Cg・Ci…6・7・8予約
(ADH・abi)…2井桁
(CDH・agi)…7井桁
と書いてあった。
ヒント1行目の下段左側3×3ブロック中6・7・8予約もしくは3国同盟は、すでに図中に反映ずみである。
私は3行目の(CDH・agi)…7井桁もしくはメカジキ法を、先に見つけた。先走って言ってしまうと、どっちが先でも解けるのだ。
いつもの着色により図示してみる。すなわち7が飛車にらみするマスを灰色で、3連井桁(CDH・agi)を構成する空白マスを濃い橙、それ以外の7を候補に含むマスを薄い橙で着色する。
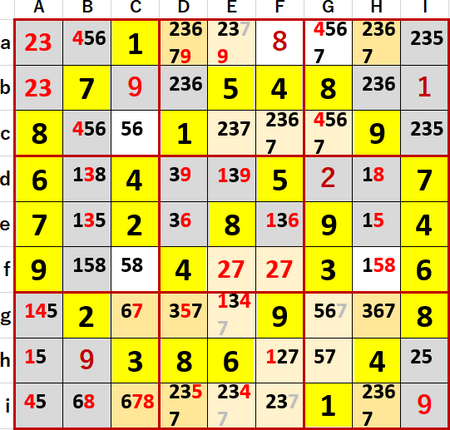
この井桁に着目することにより、空白マスEa、Eg、Ei、Fi、Ggに入る候補から7を除くことができる。「列方向の井桁を見つけ、行方向の候補を除く」処理を行った次第である。
ただし図中には除外した候補も灰色フォントで残している。これもいつもと同じ。
前図と同じ状況下では、(EFG・cfh)…7井桁というのも見つけることができる。先の(CDH・agi)は列方向に、この(EFG・cfh)は行方向に、7が候補として入るマスが3つに限定されている。
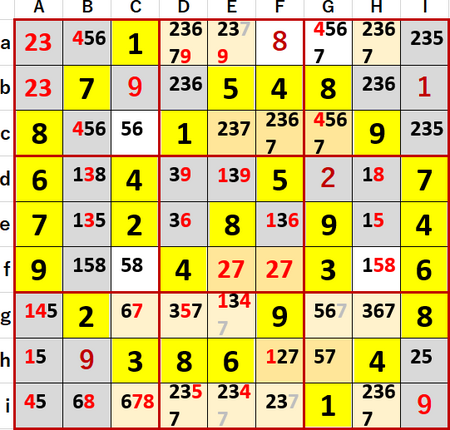
「行方向の井桁を見つけ、列方向の候補を除く」処理を行ったわけだが、Ea、Eg、Ei、Fi、Ggに入る候補から7を除くことができるという結論に変わりはない。
続いて後回しにしたヒント2行目の(ADH・abi)…2井桁を図示する。ヒント見ないで解いたぞというアピールに見えますか見えますねすみません。
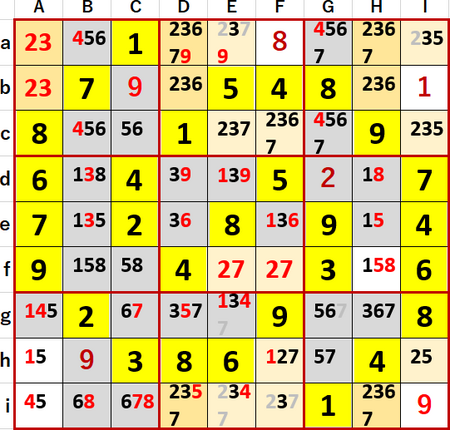
結果、Ea、Ei、Fi、Iaの候補から2を除くことができる。
前図と同じ状況では、(EFI・cfh)…2井桁も成立している。先の(ADH・abi)は列方向に、この(EFI・cfh)は行方向に、2が候補として入るマスが3つに限定されている。
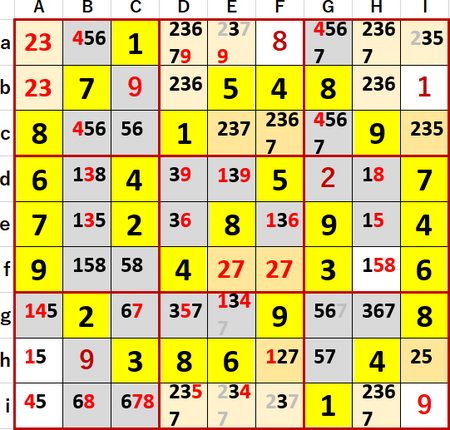
どちらを見た場合でも、Ea、Ei、Fi、Iaの候補から2を除くことができる。
ようするに、この問題でも経験則は成立していた。
中学校レベル幾何学の「二つの長方形の交点をとったら、それらの交点はどちらの長方形にも属している」というあたりまえのことをわざわざ述べていたような気もするが、自分の整理のためだからいいのだ。
ともあれ以上により空白セルFiに3が確定し、それを手がかりに多重選択の連鎖的解消が始まった。
最終形を示す。Solutions P119と一致している。