かなり昔の話になる。野崎昭弘氏のロングセラー『詭弁論理学』に、難解な論理パズルが載っていた。そのパズルに関連して奇妙な派生問題を思いつき、ネットの匿名掲示板で公開したことがあった。しかし、ほとんど反応なかった。私の説明がヘタクソだったことが主原因だろう。
だがそれを唐突に思い出し、ネットのどこかに残しておきたくなったので、少しでもわかりやすくならないかとMS-Officeの図形で作成したイラストを多用しつつ、自ブログに収録する。
【問題】
中世の小王国ナーナッパには、王様と7人の大臣がいる。大臣同士は仲が悪く、プライベートでは互いに口も利かない。
7人の大臣にはそれぞれ配偶者がいるが、みな不倫をしている。彼女らが不倫していることは、王様と夫の大臣以外の大臣全員が知っているが、夫の大臣だけが知らない。

この状況を憂いた王様は、大臣たちを集めて次のように命じた。
「汝らの奥方は不倫をしている。それがわかったら、ただちに自分で手を下せ。さもなくば朕が汝らを粛清する!」
王様の厳命に、大臣たちは震え上がった。
ナーナッパ王国には唯一の国営新聞があって、1日に1回発行されている。この新聞には国内で起きたことならネコのお産からウマの葬式まで何でも載っており、大臣宅には毎朝無料で配達されている。
大臣たちは毎日、それを目を皿にして読んだ。

1日目、何も起きなかった。
2日目、何も起きなかった。
3日目、何も起きなかった。
4日目、何も起きなかった。
5日目、何も起きなかった。
6日目、何も起きなかった。
7日目の朝、惨劇が起きた! 7人の大臣宅において新聞を読み終えた大臣は、それぞれ配偶者に対して白刃を振るったのである。

大臣たちは、どのように自分の配偶者が不貞を働いていることを推理したか、説明せよ。
元ネタは『詭弁論理学』旧版P143以降に記載されていますが、現在新刊が入手できる改版ではページが変わっている可能性があります。
また元ネタでは「40人の貴族とその従者」でしたが、訳あって大臣とその配偶者に改変しました。ポリティカル・コレクトネス的には悪化していますが、パズルということでご容赦いただきたく。
新聞にはネコのお産からウマの葬式まで載っているというところは、意味のないこだわりで原作通りです。
【解説】
アルゴリズム用語でいう「再帰呼び出し(リカーシブ)」を使います。
大臣が2人の場合
大臣が2人しかいなかったと仮定する。

大臣1の視点で考えてみる。大臣2の配偶者が不倫していることは知っているが、自分の配偶者が不倫しているか否かはわからない。大臣2も同様である。
大臣1は、まずは自分の配偶者が潔白だと仮定する。
そうすると大臣2は、ただちに自分の配偶者を仕置きするはずである。でなければ大臣2が処罰される。
そしてそのことは、王命が下って1日目の新聞に載るはずである。
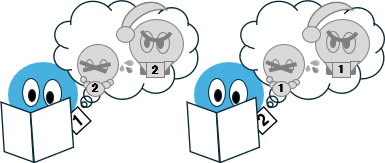
しかし、そのような報道はなかった。
このことから、大臣1は自分の配偶者もまた不貞であることを推理した。
大臣2も同様である。
かくして2日目に大臣1、大臣2の邸宅において、同時に惨劇が発生した。
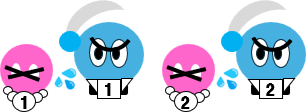
ここまでいいですか? 合ってますよね? ここまでを踏まえなければ、これ以降の議論は砂上の楼閣と化します。
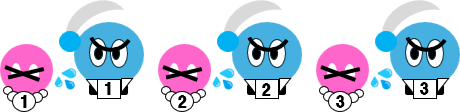
大臣3人のケース
1日目
やはり大臣1の視点で考える。大臣1には、自分の配偶者が不倫しているかどうかはわからないが、まずは配偶者が潔白であると仮定する。
そうすると、大臣2はどう考えるだろう?
大臣2は、やはりまず自分の配偶者が潔白であると仮定するだろう。さらに、もしそうなら大臣3は、王命が下った直後に配偶者に手を下すと考えるはずだ。
大臣3に関しても、同様の推論が成立する。
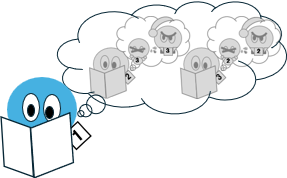
すなわち大臣1の配偶者が潔白、大臣2の配偶者が潔白であれば、大臣3は即日、自分の配偶者を仕置きしたはずであり、それが1日目の新聞に載るはずである。
だが、そのようなことは新聞に載っていなかった。
これは、大臣2にとって自分の配偶者が潔白という仮定が崩れたことを意味する。大臣3にとっても同様である。
2日目
引き続き、もし大臣1の配偶者が潔白であれば、大臣2と大臣3はそれぞれ自分の配偶者がクロであると推理するはずである。そして大臣2と大臣3は、同時に自分の配偶者に手を下すはずである。
だが、そのようなことは2日目の新聞に載っていなかった。
これにより、大臣1は自分の配偶者がクロと判断するのである。
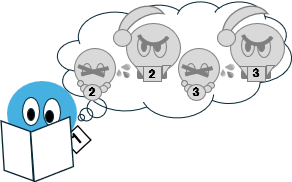
ちなみにここまでの大臣1の推論は、「大臣2人のケース」と同一である。
3日目
かくして大臣1、大臣2、大臣3宅で、同時に惨劇が発生した。
個人的な感想としては、大臣2人の場合と大臣3人の場合で、推論の難易度に段差があるように感じる。
3人の場合の1日目において、大臣1は大臣2の配偶者がクロであることを知りながら、大臣2は自分の配偶者がシロと考えるという仮定を置く。
大臣2は自分の配偶者がシロかクロかわからないのだから、決して不自然な仮定ではないはずだが、どうにも気持ち悪い。
有名な google:サリーとアンの課題 に、ちょっと似ている気がする。シチュエーションを変えると、サリーとアンの課題は健常者にとっても難問に変わるのだろうか? それとも私自身が発達障害を抱えているのか。
大臣4人のケース
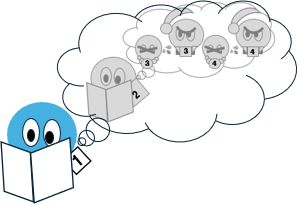
1日目
やはり大臣1は、自分の配偶者が潔白であると仮定する。
そしてやはり大臣2に着目する。
大臣2もまた、自分の配偶者が潔白であると仮定する、と仮定する。
大臣3もまた、やはりまずは自分の配偶者が潔白であると仮定するだろう。もしそうなら大臣4は、王命が下った直後に配偶者に手を下すはずである。
大臣4に関しても、同様の推論が成立する。

すなわち大臣1の配偶者が潔白、大臣2の配偶者が潔白、大臣3の配偶者が潔白であれば、大臣4は即日、自分の配偶者を仕置きするはずだ。そしてそれが1日目の新聞に載るはずである。
だが、そのようなことは新聞に載っていなかった。
これは、大臣3にとって自分の配偶者が潔白という仮定が崩れたことを意味する。大臣4にとっても同様である。
2日目
引き続き、もし大臣1の配偶者が潔白かつ大臣2の配偶者が潔白であると仮定すれば、大臣3と大臣4はそれぞれ自分の配偶者がクロであると推理するはずである。そして大臣3と大臣4は、同時に自分の配偶者に手を下すはずである。
だが、そのようなことは2日目の新聞に載っていなかった。
これにより、大臣2は自分の配偶者がクロと判断するのである。
3日目
もし大臣1の配偶者が潔白なら、大臣2、大臣3、大臣4は同時に自分の配偶者に手を下すはずである。
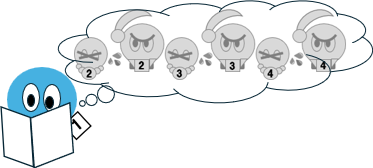
だが、そのようなことは3日目の新聞に載っていなかった。
これにより、大臣1は自分の配偶者がクロと判断するのである。
ちなみにここまでの大臣1の推論は、「大臣3人のケース」と同一である。
このように「ケースnの場合の推論」を用いて「ケースn+1の場合の推論」を導くのが、再帰呼び出し(リカーシブ)の考え方である。
再帰呼び出しを用いることにより、プログラムの記述を簡潔化できることがある。ただし再帰呼び出しで、プログラム自体の処理が高速化されるわけではない。場合によっては、処理が爆発的に増大することさえある。有名な事例に google:ハノイの塔 がある。
4日目
かくして大臣1、大臣2、大臣3、大臣4宅では…

大臣5人のケース、大臣6人のケース、大臣7人のケースは省略せざるを得ないが、同様の手順により5日目、6日目、7日目に惨劇が発生するという結論が導かれるのである。
ご理解いただけましたでしょうか?
元ネタの「40人のケース」は、もし論証の過程を丹念に記述しろと言われたら「やってられるか~ヽ(`Д´)ノ」とならざるを得ない。どこかで省略せざるを得ない。
何より7人の大臣や元ネタの40人の貴族が、一概にこれだけの論理的推論を展開できる能力を持っていると仮定する必要がある。
野崎『詭弁論理学』や続編の『逆説論理学』、あるいはパウンドストーン『ビル・ゲイツの面接試験―富士山をどう動かしますか?』には、このような論理パズルが数多く収録されている。
『ビル・ゲイツの面接試験』には、「"完全に論理的な存在"(Perfectly Logical Being:PLB) は普通の人間と違う」と題された節があった。
人間の行動は、いつもどこかに不確実なところがある。PLBの行動はそうではない。そのため、これらのパズルで意図されている解は、ひどく非現実的だ。Aはしかじかと考えるとBは考えているとCは考えているとDは考えている……という形をとるのが一般的だ。現実の世界ではそんな動き方をするものはない。
『ビル・ゲイツの面接試験』P169
ですよねー。
実際「もしわかってない奴が一人混じっていたら」と仮定すると、さらにグロい展開が生じる。それを私のオリジナルの部分として、「後編」として述べる予定である。
追記:
「後編」ではなく「中編」を書きました。


